8556. Chain

Given a sequence of n integers a₁, a₂, ..., a_n. For any element a_k (k = 1, 2, ..., n) we find the first larger than a_k element, which is placed to the right of a_k (if such exists). Denote it by a_k1. Then do the same with a_k1 and denote the found element by a_k2, and so on until we run out of the given sequence. Thus formed subsequence a_k1, a_k2, ..., we call chain beginning at index k.

Write a program that outputs for any index k the length of the corresponding chain that starts at index k.

Input. The first line contains positive integer n (0 < n ≤ 500000). The second line contains the elements of the given sequence a₁, a₂, ..., a_n (0 < a_i < 10⁶).

Output. Print in one line the sequence of chain’s lengths, corresponding to the elements of the input data.

Sample input	Sample output
10 3 2 4 2 11 2 7 5 8 10	2 2 1 1 0 3 2 2 1 0

SOLUTION

stack

Algorithm analysis

Declare an array nex such that nex[i] contains the index of the closest to the right element greater than a_i. For example, nex[i] = 0 means that there are no elements to the right of a_i greater than a_i.

Declare a stack s that will store indices i instead of numbers a_i. Push the first item onto the stack: s.push (1) – push the index of the first item. Process sequentially the rest of the sequence numbers. Let the current element be a_j. Then:

· if a[s.top()] ≥ a[j], push index j into the stack: s.push(j);

· otherwise, until the stack is not empty and a[s.top()] < a[j], pop element from the stack i = s.top() and set nex[i] = j. Upon completion of the loop push j into the stack: s.push(j);

Now, from the nex array, the resulting sequence dp should be reconstructed, where dp[i] equals to the length of the chain starting from index i.

· if nex[i] = 0, then dp[i] = 0;

· otherwise dp[i] = dp[nex[i]] + 1;

Example

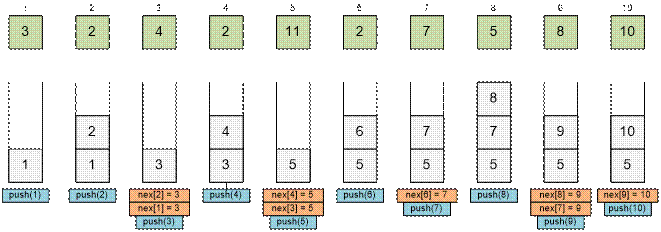
Fill the array dp from right to left.

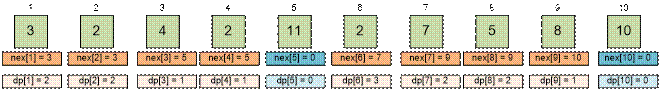
Algorithm realization

Declare the arrays.

#define MAX 500001

int a[MAX], nex[MAX], dp[MAX];

stack<int> s;

The main part of the program. Read the input data.

scanf("%d",&n);

for(i = 1; i <= n; i++)

scanf("%d",&a[i]);

Push to the stack the index of the first element – one.

s.push(1);

Sequentially process the rest of the elements.

for(j = 2; j <= n; j++)

{

while(!s.empty())

{

i = s.top();

if(a[i] >= a[j]) break;

nex[i] = j;

s.pop();

}

s.push(j);

}

Recalculate the resulting array.

dp[n] = 0;

for(i = n - 1; i >= 1; i--)

if (nex[i] == 0) dp[i] = 0;

else dp[i] = 1 + dp[nex[i]];

Print the answer – the lengths of the chains starting from position i.

for(i = 1; i <= n; i++)

printf("%d ",dp[i]);

printf("\n");

Java realization

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int a[] = new int[n+1];

int next[] = new int[n+1];

int dp[] = new int[n+1];

for(int i = 1; i <= n; i++)

a[i] = con.nextInt();

Stack<Integer> s = new Stack<Integer>();

s.push(1);

for(int j = 2; j <= n; j++)

{

while(!s.empty())

{

int i = s.peek();

if(a[i] >= a[j]) break;

next[i] = j;

s.pop();

}

s.push(j);

}

dp[n] = 0;

for(int i = n - 1; i >= 1; i--)

if (next[i] == 0) dp[i] = 0;

else dp[i] = 1 + dp[next[i]];

for(int i = 1; i <= n; i++)

System.out.print(dp[i] + " ");

System.out.println();

con.close();

}

}